Trigonometry Study Materials PDF With Practice Questions Worksheet

Trigonometry Study Materials PDF: The most important task of trigonometry is to find the remaining side and angle of a triangle when some of its side and angles are given. This problem is solved by using some ratio of sides of a triangle with respect to its acute angle. This ratio of acute angle are called the trigonometric ratio of angle. Let us now define various trigonometric ratio.

Trigonometry Study Materials PDF For Competitive Exams

Article Name	Trigonometry Study Materials PDF With Practice Questions Worksheet
Category	Study Materials
Name Of The Lesson	Trigonometry
Name Of The Subject	Mathematics
Important For	Competitive Exams & Other Exams
Post Included	Important Formulae, Notes, Study Materials, Practice Questions Worksheets PDF
Quality	Best
Format	PDF
Official Website	https://www.educationlearnacademy.in/

Contents

Trigonometry Basics
1. Six Important Trigonometric Functions
Trigonometry Ratios Table
Trigonometry Formula
Trigonometry Questions & Answers For Competitive Exams
Trigonometry Problems & Solutions
Height And Distance
1. Line of Sight
Trigonometry Practice Questions Worksheet PDF
Trigonometry Frequently Asked Questions

Trigonometry Basics

The concept of Trigonometry is given by a Greek mathematician Hipparchus. Trigonometry is all about a right-angled triangle.

It is one of those divisions in mathematics that helps in finding the angles and missing sides of a triangle by the help of trigonometric ratios.

The angles are either measured in radians or degrees. The usual trigonometry angles are 0°, 30°, 45°, 60° and 90°, which are commonly used.

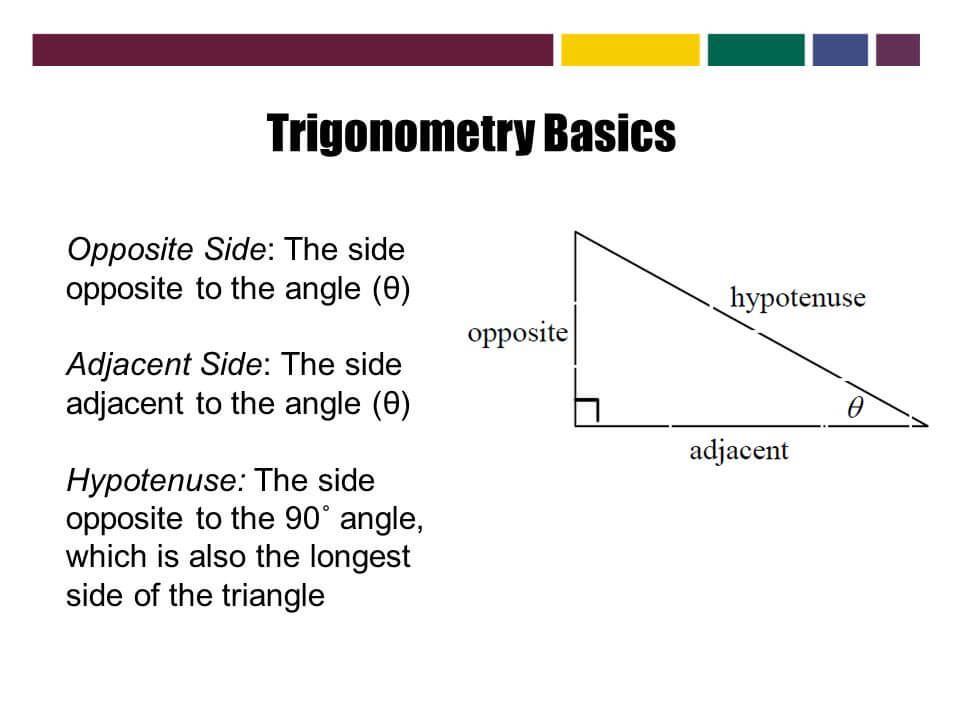
Six Important Trigonometric Functions

The six important trigonometric functions (trigonometric ratios) are calculated by the below formulas using above figure. It is necessary to get knowledge regarding the sides of the right-angle triangle because it defines the set of important trigonometric functions.

Functions	Abbreviation	Relationship to sides of a right triangle
Sine Function	sin	Opposite side/ Hypotenuse
Tangent Function	tan	Opposite side / Adjacent side
Cosine Function	cos	Adjacent side / Hypotenuse
Cosecant Function	cosec	Hypotenuse / Opposite side
Secant Function	sec	Hypotenuse / Adjacent side
Cotangent Function	cot	Adjacent side / Opposite side

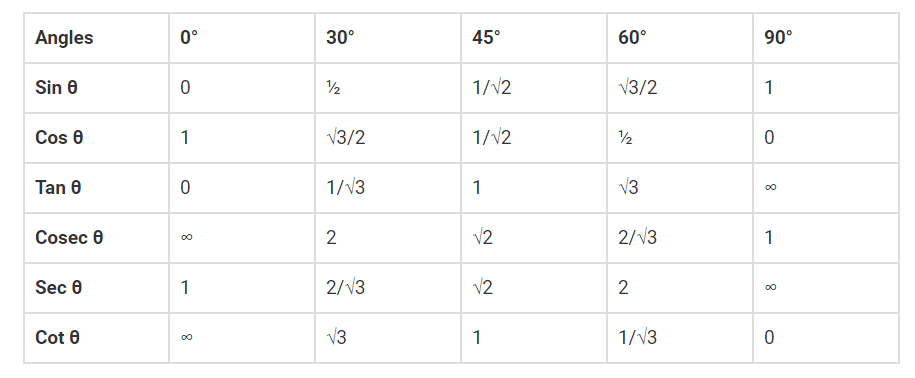
Trigonometry Ratios Table

The standard angles of trigonometrical ratios are 0°, 30°, 45°, 60° and 90°. The values of trigonometrical ratios of standard angles are very important to solve trigonometrical problems.

The values of trigonometrical ratios of standard angles are very important to solve the trigonometrical problems. Therefore, it is necessary to remember the value of the trigonometrical ratios of these standard angles. The sine, cosine and tangent of the standard angles are given below in the table.

Trigonometry Formula

The Trigonometric formulas or Identities are the equations which are true in the case of Right-Angled Triangles. Some of the special trigonometric identities are as given below –

1. Pythagorean Identities

sin ² θ + cos ² θ = 1
tan ² θ + 1 = sec² θ
cot² θ + 1 = cosec² θ
sin 2θ = 2 sin θ cos θ
cos 2θ = cos² θ – sin² θ
tan 2θ = 2 tan θ / (1 – tan² θ)
cot 2θ = (cot² θ – 1) / 2 cot θ

2. Sum and Difference identities-

For angles A and B, we have the following relationships:

sin(A + B) = sin(A)cos(B) + cos(A)sin(B)
cos(A + B) = cos(A)cos(B) – sin(A)sin(B)
tan(A + B) = tan(A) + tan(B)/1−tan(A) tan(B)
sin(A – B) = sin(A)cos(B) – cos(A)sin(B)
cos(A – B) = cos(A)cos(B) + sin(u)sin(v)
tan(A – B) = tan(A) − tan(B)/1+tan(A) tan(B)

3. If A, B and C are angles and a, b and c are the sides of a triangle, then,

Sine Laws

a/sinA = b/sinB = c/sinC

Cosine Laws

c² = a² + b² – 2ab cos C
a² = b² + c² – 2bc cos A
b² = a² + c² – 2ac cos B

Trigonometry Formula PDF in Hindi

Trigonometry Questions & Answers For Competitive Exams

Here we have attached some Trigonometry questions and their solutions for competitive exams like SSC, Railway, UPSC & other exams.

Question 1: In a ΔABC right angled at B if AB = 12, and BC = 5 find sin A and tan A, cos C and cot C

Solution:

AC=√((AB)^2+(BC)^2 )
=√(〖12〗^2+5^2 )
=√(144+25)
=√169=13

When we consider t-ratios of∠A we have
Base AB = 12
Perpendicular = BC = 5
Hypotenuse = AC = 13
sinA=Perpendicular/Hypotenuse=5/13
tanA=Perpendicular/Base=5/12

When we consider t-ratios of ∠C, we have
Base = BC = 5
Perpendicular = AB = 12
Hypotenuse = AC = 13

cosC = Base/Hypotenuse = 5/13
cotC = Base/Perpendicular = 5/12

Question 2 : Find the value of 2 sin2 30° tan 60° – 3 cos2 60° sec2 30°

Solution:
2(1/2)^2×√3-3(1/2)^2×(2/√3)^2
=2×1/4×√3-3×1/4×4/3=√3/2-1=(√3-2)/2

Question 3 : In a right triangle ABC right angle at B the six trigonometric ratios of ∠C

Solution:
sinA=Perpendicular/Hypotenuse=3/5

Base=√((Hypotenuse)^2-(Perpendicualr)^2 )
=√(5^2-3^2 )
=√(25-9)=√16=4

Now
sinC=BC/AC=4/5,cosecC=5/4
cosC=3/5=AB/AC,secC=5/3
tanC=AB/AC=4/3,cotC=3/4

Question 4 : Find the value of 2 sin2 30° tan 60° – 3 cos2 60° sec2 30°

Solution:
2(1/2)^2×√3-3(1/2)^2×(2/√3)^2
=2×1/4×√3-3×1/4×4/3=√3/2-1=(√3-2)/2

Question 5 : bFind the value θ sin2θ=√3

Solution:
sin2θ= √3/2
2θ = 60
θ = 30°

Question 6 : Find the value of x. Tan 3x = sin 45° cos 45° + sin 30°

Solution:
tan3x=1/√2×1/√2+1/2
=1/2+1/2=1
⇒tan3x=1 ⇒ tan3x = tan45°
3x = 45°
X = 15°

Trigonometry Problems & Solutions

Practice these questions given here to get a deep knowledge of Trigonometry. Use the formulas and table given in this article wherever necessary.

Q.1: In △ABC, right-angled at B, AB=22cm and BC=17cm. Find:

(a) sin A Cos B

(b) tan A tan B

Q.2: If 12cot θ= 15, then find sec θ?

Q.3: In Δ PQR, right-angled at Q, PR + QR = 30 cm and PQ = 10 cm. Determine the values of sin P, cos P and tan P.

Q.4: If sec 4θ = cosec (θ- 300), where 4θ is an acute angle, find the value of A.

Height And Distance

Sometimes, we have to find the height of a tower, building, tree, distance of a ship, width of a river, etc.

Though we cannot measure them easily, we can determine these by using trigonometric ratios.

Line of Sight

The line of sight or the line of vision is a straight line to the object we are viewing. If the object is above the horizontal from the eye, we have to lift up our head to view the object. In this process, our eye move, through an angle. This angle is called the angle of elevation of the object.

If the object is below the horizontal from the eye, then we have no turn our head downwards no view the object. In this process, our eye move through an angle. This angle is called the angle of depression of the object.

Example: A 25 m long ladder is placed against a vertical wall of a building. The foot of the ladder is 7m from base of the building. If the top of the ladder slips 4m, then the foot of the Ladder will slide by how much distance.

Sol: Let the height of the wall be h.

Now, h = √(〖25〗^2-7^2 )
= √(576 ) = 24m
QS = √(625-400)
= √(225 )=15m
Required distance, X = (15-7) = 8m

Trigonometry Practice Questions Worksheet PDF

Here we have attached the trigonometry practice questions pdf along with the trigonometry worksheet pdf. You can also download Complete Trigonometry Study Materials PDF from the table given below:

Trigonometry Study Materials & Worksheets PDF	Download PDF
Trigonometry Study Materials & Formulae PDF	Download
Trigonometry Practice Worksheet PDF	Download
Trigonometry SSC CGL 2011 to 2018 Questions PDF	Download

Trigonometry Frequently Asked Questions

What do you Mean by Trigonometry?
Ans. – Trigonometry is one of the branches of mathematics which deals with the relationship between the sides of a triangle (right triangle) with its angles. There are 6 trigonometric functions to define It.

What are the Different Trigonometric Functions?
Ans. – The 6 trigonometric functions are: Sine function, Cosine function, Tan function, Sec function, Cot function, Cosec function

Who is the Father of Trigonometry?
Ans. – Hipparchus was a Greek astronomer who lived between 190-120 B.C. He is considered the father of trigonometry.

What are the Applications of Trigonometry in Real Life?
Ans. – The real life applications of trigonometry is in the calculation of height and distance. Some of the sectors where the concepts of trigonometry is extensively used are aviation department, navigation, criminology, marine biology, etc.